Research
I am an applied mathematician with interests in complex systems and mathematical biology. I use modeling, analysis, and computer simulation of differential equations systems to both provide insight and make predictions about biological and physical phenomena.
Pattern formation in complex systemsWe study the effect of connectivity between randomly behaving agents representing, e.g., fireflies flashing, neurons firing, and crowds applauding. Using a combination of numerical simulations and mathematical analysis, we investigate how the strength of interactions and the network of connections between the agents leads to a large variety of patterns and synchronization between the agents. This work has applications in biological systems, neuroscience and social sciences. Press: TCNJ Magazine, Winter 2020 |
Click here for more movies! 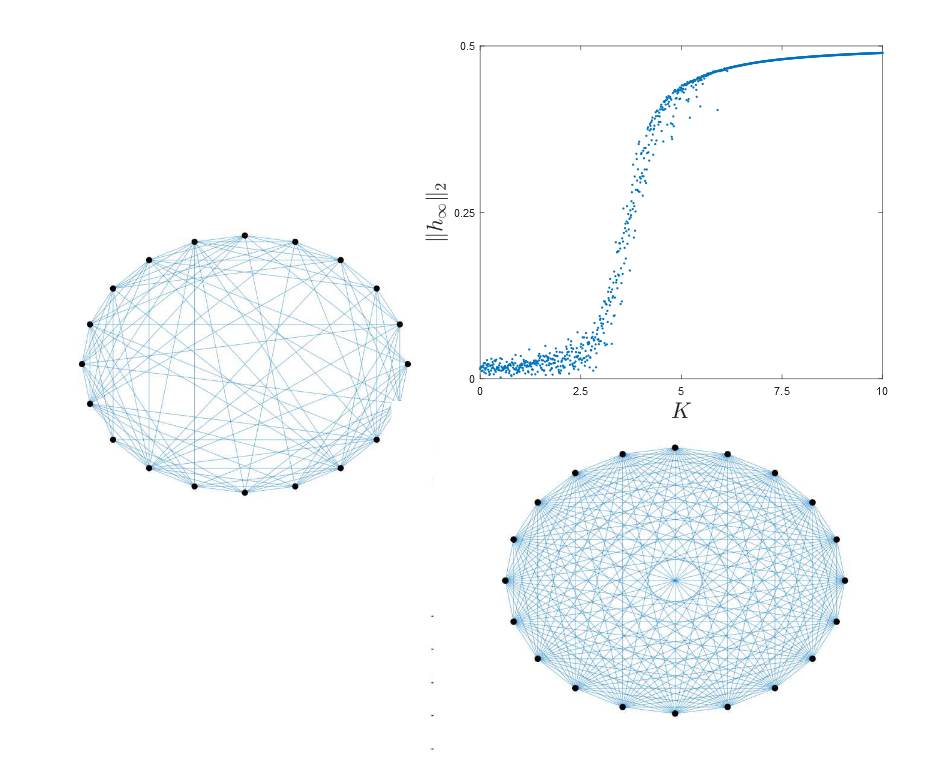
|
|---|---|

|
Crawling cell motility
|