CHAPTER 9

Stellar Spectral Classes and the H-R Diagram

A. Stellar Spectral Classes
      In 1893, the Harvard College Observatory undertook a project of
photographing and cataloging the spectra of several hundred thousand stars.
This project was supported by an endowment from Henry Draper, a wealthy
physician. The spectra were assigned a classification based on the relative
strengths of the Balmer absorption lines seen in a star's spectrum. The
Balmer lines make up a series of spectral lines produced by hydrogen in the
visible spectrum. The assumption was that the strength of the Balmer
lines indicated the abundance of hydrogen atoms in the atmosphere of a star.
The stars that displayed the strongest Balmer lines were classified as Type A.
Letters were then assigned for decreasing strength of the lines., viz., B, C, D,
etc.
    In 1920, the Indian astrophysicist Meghnad Saha developed the atomic
theory indicating that specral line strength was mostly determined by the
temperature in a star's atmosphere rather than abundance. Abundance had
only a secondary role in determing line strength.   It was then decided to place
the spectral classes in order of temperature. To accomplish this, some of the
spectral classes, like C and D, were combined with other classes thereby
eliminating these letters. In addition, the surviving spectral types were
subdivided into decades to allow for a more precise determination of
temperature.   For example, the sequence B1, B2, B3, ... up to B9 indicated
decreasing temperature in the star's atomosphere.
     The most common spectral classes now are:

O, B, A, F, G, K, and M.

In this sequence, the hottest stars are O stars and the coolest stars are M stars.
A B0 star is slightly hotter than a B1 star and an A5 star is somewhat hotter
than an A7 star. For example, the Sun's spectral class is G2. Therefore,
spectral class is often used as a surrogate for temperature.
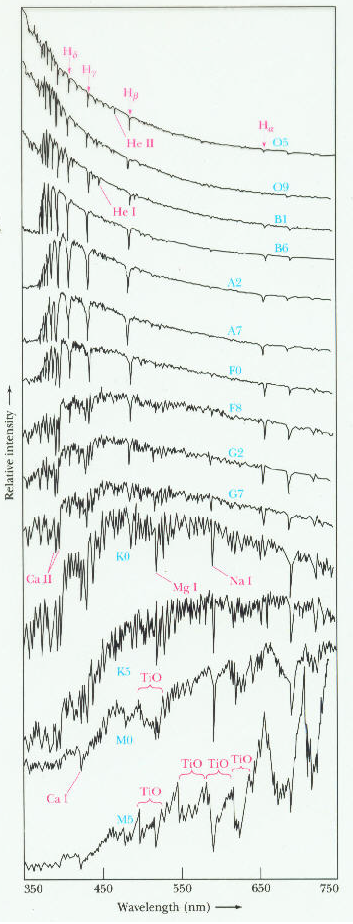
    The following diagram shows a raster of different stellar spectra showing the
absorption line strenths change from one spectral class to another. The top
spectrum shows the spectrum of a vey hot star, classified as O5. The last
spectrum is for an M5 star, which is by comparison, very cool.   Note the
appearnace of TiO spectral bands in the coolest stars and the numerous
unionized metallic lines.   The strenth of the Balmer lines, which belong to
hydrogen, are the strongest at spectral type A2.

B. Theory of the Differences in Stellar Spectra

The strengths of the absorption lines in a stellar spectrum depend mainly on the
temperature of a star's lower atmosphere (chromsophere) and secondarily on the
abundance of an element, but in a complex way. Temperature determines what stages
of ionization for a given atom will exist in a stellar atmosphere as well as the degree of
excitation for that stage of ionization. Ionization and excitation (getting electrons into
higher energy states) result from the collisions among the atoms and the absorption of
photons of radiation.

Neutral Hydrogen (H I) is difficult to excite at low temperature because its single electron
is very tigntly bound in its ground state. Therefore its spectral lines are weak in stars cooler
than 5000K. For higher temperature stars, the Balmer lines become stronger, reaching a
peak strength at spectral type A2. For even hotter stars, the number of ionized hydrogen
atoms (H II) increases over the number of H I atoms and so the Balmer lines get weaker.
H II can not produce any absorption lines, since it has no electrons.

A similar remark can be made for He. However, He II lines are possible at very high
emperatures, since He II still has one elctron..

Metals like Ca, Mg, Fe, Na, etc., have loosely bound outer electrons which are capable of undergoing
collisional and photoexcitation (absorbing photons) at low stellar temperatures. So these lines dominate the
spectra of cool stars. For the hotter stars, the neutral metallic atoms become ionized and the absorption lines
of these ionized atoms, like Ca II, begin to dominate a star's spectrum.

From the above theory, there is now a kown calibration between spectral class and a star's surface temperature.

^{C. Summary
of Determining Stellar Temperatures}

With the above theory, it then becomes possible to determine the surface temperature
of a star by using the ratio of the strengths of different absorption lines in a star's spectrum.
This is more accurate than using Wien's Law or by using the calibration between the B-V color index
and temperture.

Let's summarize then, the different ways to determine the temperature of a star:

1. Using the Stefan-Boltzmann law, if one is able to measure the total energy radiated by a star
over the entire spectrum. However, this is not practical to do because of the many absorption lines
in the spectrum and no one instrument can measure the radiation of stars over the entire spectrum.

2. Determine the wavelength of maximum brightness in the star's spectrum and apply Wien's Law.

3. Measure the B and V magnitudes of a star and look up the calibrated B-V color index versus
temperature relation. See the previous chapter for details

4. Measure the relative strengths of the different absorption lines in a star's spectrum and use the
atomic theory of excitation and ionization to determine the temperature. This is the most accurate
method.

^{D. The Hertzsprung
- Russell Diagram}

Between 1908 and 1913, E. Hertzsprung, a danish astronomer, and H. N. Russell in the US,
independently compiled absolute magnitudes and temperatures for many stars and displayed this
information graphically. Such a graph, where M is plotted versus spectral class or temperature,
is now called an H-R Diagram. Sometimes luminosity replaces absolute magnitude and the diagram
is often referred to as temperature-luminosity diagram. Such a diagram is schematically reprsented
below.

^{SCHEMATIC H-R DIAGRAM}

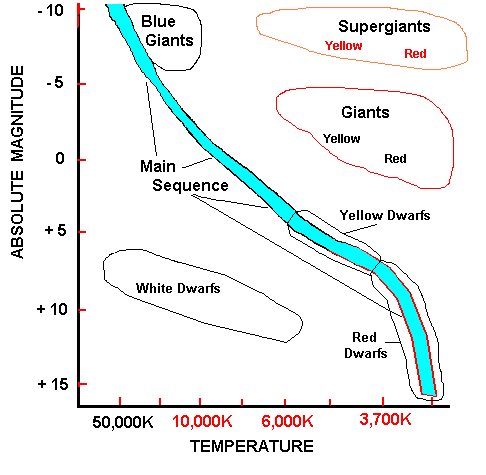
Remember, to plot a point for a star in the H-R Diagram, one must know the absolute magnitude and
temperature or spectral class of the star. The temperature may be determined by studying the spectrum
of the star. However, one can not measure the absolute magnitude of a star, it can only be calculated.
There are more than 2,000 stars for which this can be done and they are all within 100 parsecs of the Sun.

In the H-R Diagram, one does not find a random distribution of points that represent the stars.
Instead, the points, one for each star, fall into distinct groups on the chart. Most of the stars appear to
fall along a locus that was called the main sequence. Other groupings are identified as white dwarfs, giants,
supergiants, etc. It is now realized that all of these groupings represent relatively long-lived stages of
stellar evolution.

The longest-lived stages of evolution are the white dwarf and main sequence stages. Therefore,
statistically, one finds a larger number of stars in these stages of evolution than any of the other stages.

Stars on the main sequence are delineated by mass. That is, stars of different mass, but in the main
sequence stage of evolution, do not fall at the same point in the diagram but are spread out over the
locus labeled as the main sequence in the above diagram. The least massive stars fall at the bottom of
the main sequence and are also called red dwarfs. As we move up along the main sequence, we find
stars of greater mass, such as the yellow dwarfs. The Sun is a yellow dwarf main sequence star. Stars
with masses greater than the Sun's are found yet higher on the main sequence. The most massive main
sequence stars are those found at the top, adjacent to the Blue Giants.

Notice that as one moves up along the main sequence, the mass and brightness of the star are
greater. This is known as the

Mass-Luminosity Law:

The greater the mass of a main sequence star, the brighter it is.
(Memorize this and be able to apply.)

This law does not apply to any other stars such as, the white dwarfs or giant stars.

^{E. Determining
Stellar Masses}

The only way the mass of a body can be determined is by observing its gravitational interaction
with another body. Hence, it is not possible to determine the masses of single stars. It is through the
study of the motions of stars in a binary system that the masses of these stars have been determined.
Since more than 50% of all stars are binary systems, it has been possible to determine the masses of a
goodly number of stars.

Range of Stellar Masses: The most massive stars are about 110 times more massive than the Sun.
Stars more massive than this tend to be very unstable. The least massive stars have 0.06 or 0.07
solar mass units (the Kumar Limit for TNF to occur).

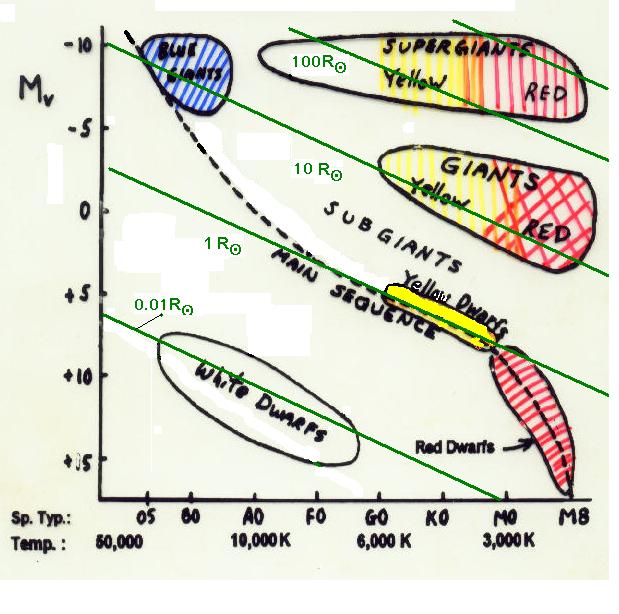
F. Luminosity Classes

The luminosity classes are loci in the H-R diagram as shown below in Fig. 3, below. Luminosity class can be
assigned by studying the widths of the absorption lines in a star's spectrum. Read about this in the text.

The luminosity classes are:

    I   The supergiants
    II The bright giants
    III The giants
    IV The sub-giants
    V   Main sequence star
    VI   Sub-dwarfs
    VII White Dewarfs

G. Spectroscopic Parallax

By determining both the spectral type and luminosity class, a star's location in the H-R Diagram
may be determined without knowing the absolute magnitude a priori. For example, a K2 III star
could be located in the H-R diagram as a point on the locus labeled III, and hence, that star's absolute
magnitude may be read from M-scale.
This method is used for finding the distance of a star that is too far away to have its
trignometric parallax measured. From an examination of a star's spectrum, one may deduce the star's
spectral type and luminosity class. The luminosity class is discerned by examining the absorption
lines in a star's spectrum. . Knowing the spectral type and luminosity class of the star, the H-R diagram is
used to determine the star's absolute magnitude. This and the apparent magnitude of the star allow the
distance of the star to be computed, using the inverse square law for light.

    Distance Modulus, m-M
        a. If negative, star is closer than 10 parsecs
        b. If zero, star is at 10 parsecs
        c. If positve, star is farther than 10 parsecs

The exact distance of the star may be calculated using the inverse square law for light. This
results in the relation:

M = m + 5 - 5log(d),

where d is the heliocentric distance of a star in parsecs. So when M and m are known, the above
equation be used to solve for d.

Using Fig. 3 below, we determine that the absolute magnitude of a K2 III star is M= +0.3. If the apparent
magnitude is measured, one may now compute the distance modulus of the star or the actual distance using
the equation above.

Refer to class notes for a sample problem worked out in class. Also read Ex. 18.7 in the
Course Manual.

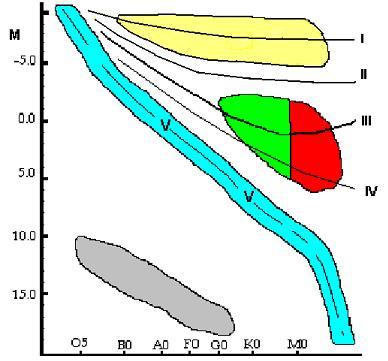
Fig. 3

Anothr example: A spectral analysis of the star Arcturus indicates that it is a K2 III star.
Its apparent visual magnitude has been measured to be 0.50. Use the spectroscopic
parallax method to compute the distance:

From the above H-R diagram, we read off that the absolute visual magnitude of the star
is about M = 0.02. Hence the distance modulus of the star is m-M = 0.05 - 0.02 = 0.03.
We then substitute this into:

d = 10^{[ (m-M)/5.0 +1]} = 10^{[(0.03)/5 +1]} = 10 ^{[ 0.0060 +1]} = 10 ^(1.006) = 10.1 pc